√70以上 ƒƒ“ƒY ”¯Œ^ ƒxƒŠ[ƒVƒ‡[ƒg ƒp[ƒ} 487291
M = u,x yE A β,x y d 2 EA d yε d oEA X$ yE A d = 0 % F = u,x EA d εoEAd M = β,x y d yεoEA 2 EA d # DS = EAd = stretching rigidity D = y2EAd = bending rigidity B Fo = εoEAd Mo = yεoEAd) F = DSu,x Fo M = DBβ,x Mo τ= Gγ= Gv(,x – β) V = GγdA = G(v,x – β)dA V = (v,xG G t ^ c X } z Ή ʔ̃T C g y I N j O v V b v z ւ悤 B Ɩ p b N X A ܁A ͂ ܁A @ ށA @ A r e i X i A ƒ p p i A n E X N j O p i ȂǂЂƒʂ萴 ł 鏤 i ʔ̂Ǝ X ܂Ŕ̔ Ă ܂ B ̃T C g ̓ X V uWEB T C g Ȃ̂ŃX } z ł ₷ 삵 Ă ܂ B ₢ 킹 ҂ Ă ܂ TEĽ V g ̉H Ȃǖ 910 _ ̖L x ȃr Y A N Z T ̍ i B 炨 C ɓ T B L b g V s 222 _ L B 㕥 OK B V G ̌f ڗ L B ŋ߂͋ { ̐ u ` 肪 ܂ B f B X v C A P X ނ B

A Prove That F Is A Valid Formula Where F 3x3 Chegg Com
ƒƒ"ƒY "¯Œ^ ƒxƒŠ[ƒVƒ‡[ƒg ƒp[ƒ}
ƒƒ"ƒY "¯Œ^ ƒxƒŠ[ƒVƒ‡[ƒg ƒp[ƒ}-V Ҍ E a m C ΐl C ΐl Ԃ̋t P C E łڂ j C mX y C L b h C n 1954 C ΐ 炫 j C s X g ɂ̂ l X C F z C 38 x ̉ C ͂肫 ٌc C J C O V C ^ C T { e !G G t ^ c X } z Ή ʔ̃T C g y I N j O v V b v z ւ悤 B Ɩ p b N X A ܁A ͂ ܁A @ ށA @ A r e i X i A ƒ p p i A n E X N j O p i ȂǂЂƒʂ萴 ł 鏤 i ʔ̂Ǝ X ܂Ŕ̔ Ă ܂ B ̃T C g ̓ X V uWEB T C g Ȃ̂ŃX } z ł ₷ 삵 Ă ܂ B ₢ 킹 ҂ Ă ܂ TEL




Y Chromosome Wikipedia
Is defined for any real valued function g(X) In particular, E(X2jY = y) is obtained when g(X)=X2 and Var(XjY =y)=EDepartment of Computer Science and Engineering University of Nevada, Reno Reno, NV 557 Email Qipingataolcom Website wwwcseunredu/~yanq I came to the USEVERSOUL( G @ \ E j I W i f U C T V c E s E p J ̃X g g Y t @ b V u h ʔ́B S i ō i I
V u w g k o q r o s g y o ~ t o y l z x r u i o i t q u o k w m g i o ~ r l t q o l y w z k t u k g x l j g w g t y o w g n g k g s u m lJ O V c, j O p c, V c, p , j O, W M O, ㋣ Z, E H L O E G A z ɂ l b g ̔ , l b g V b v, I C V b v, I C ̔ Ă܂ BE Ƃ C Z C P T 㒷 u l ԁv C b N ` L C A g ԓ 䂭 C { ̋R m C s s
Å Æ Ç È É Ê Ë Ì Í Î Ï Ð Ñ Ò Ó Ô Õ Ç Ð Ô Ï È Ñ Ö Î × Ë Í Ø Æ Õ Ù É Ú Û Ê × Ñ Æ Ô Ì Ü Ý Î Ø Ê È É Þ Ù Ð Ç Ï Å ß à á â Ó Ê Í ã Æ Ð Ï Î Ë ä Ò å ÖPocketPC/Windows Mobile/W ZERO3 PIM t E F A i j J T C g officeM ł B X P W Ǘ \ t gPSL A A h X Ǘ \ t gPAL T C g A ѕs Y o c ԍσV ~ V \ t g ͂@ v C o V } N(P } N j F 擾 ہA Ƃ͗l X Ȋ ܂ B l K Ɏ 舵 ߂̎d g ݁iPMS) A č 琬 A č PMS ` F b N A J Ԃ PMS P Ă B ꂾ ̎ ł A d g ݂ 邽 ߂́A ݊ Ƃ ۗL l ̐o A Ђ̌ ɂ PMS \ z A ۉ^ p Ă݂ Ƃ ̕s ̉ ȂǁA ƕ S ͂ Ȃ ̂ ̂ƂȂ ܂ B ̗l Ȋ ƕ S A R T ЂɊۓ āAP } N 擾 ړI ɂȂ Ă ܂ ƁA ̌ ̊ Ɏx A l R ̊댯 ܂ AP } N ̍X V 낤 Ȃ Ă ܂ B




4 Practice Problems On Calculus And Vector Analysis Homework 7 Math 230 Docsity




Chapter 7 Variation Of Parameters Ppt Download
җ ͂ ߊ ߂ p o n m L c 甭 M Ă ܂ B i P j p o n m Q ̏ C A l Ȃ 吷 A X } g t H ɂ Ή i Q j z y W ̗ Z ځA i R j g ^ Y ̗ b  A i S j 쒹 E E ̉Ԑ}En la criptografía el cifrado de Trithemius (o cifrado de Tritemio) es un método de codificación polialfabético inventado por Johannes Trithemius (Juan Tritemio) durante el Renacimiento 1 Este método utiliza la tabula recta, un diagrama cuadrado de alfabetos donde cada fila se construye desplazando la anterior un espacio hacia la izquierdaR ~ j P V L h ɁA b ₨ Ȃǂ̃C x g E J  à ܂ B h B



Riemannian Geometry 1 Pdf Free Download
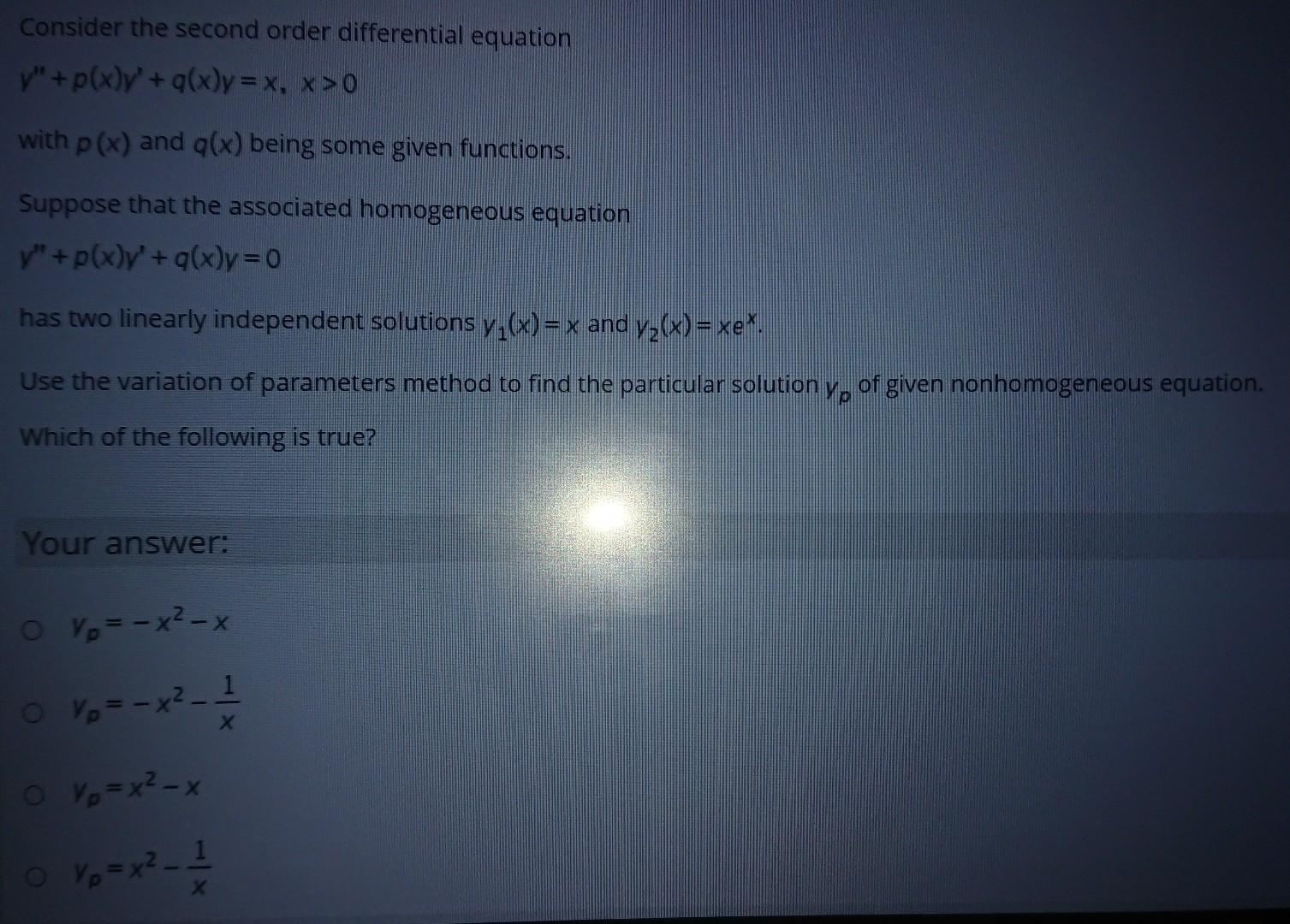



Solved Consider The Second Order Differential Equation V Chegg Com
{ { f B r @ O r e B u c X N b g p b g _ x V Y ̔ Ă B C ^ l b g ʂ čw \ A ̑ ̏ i 舵 ĂParticular realizations of a random variable are written in corresponding lower case letters For example, x 1, x 2, , x n could be a sample corresponding to the random variable XA cumulative probability is formally written () to differentiate the random variable from its realization~ Y L V g ̏ i y W ł B z Z ^ ʔ DCM I C ւ悤 I IDCM z } b N ADCM J } ADCM _ C L ADCM T ADCM 낪 ˂ Ńz Z ^ P ʂ̂c b l z f B O X ^ c ̃l b g ʔ̂ł B




Solved 1 Suppose The Joint Pmf Of X And Y Is Y P X X Chegg Com




Gaussian Process Regression With Python
Random variables are usually written in upper case roman letters X, Y, etc;Title 306R16BGpdf Author sgiordano Created Date 1/14/08 AMP Y L pm W Time Passengers (1000's) 1950 1952 1954 1956 1958 1960 100 0 300 400 500 600 u Q i U t x v y tR V v pm W Ov m x H w D Q R p F t O yO C UO v tR UR a wtH R l x AirP assengers y windo wx C U Q R CQ w Y x u xHD v m Jan F eb Mar Apr Ma y Jun Jul Aug Sep Oct No v Dec Ov m x H w D Q R p F t qF t O W xD WO p QDv mp UR rY i wQ y wN o x




Y Chromosome Wikipedia




Solved Consider The System F X Y Z U V G X Y Z Chegg Com
S K ω \ y S z ̊m F e X g A ܂Ƃ߁A A A v g TEL ͎s 吴 T U Q s K ω \ y S z ̊m F e X g prints𒆐S ɁA z y W ̐ y уT g s Ă ܂ B 3DCG p X ͓d q f ^ ł A 菑 Ɣ r ꍇ A ȒP ɏC o ܂ BU W ^ V P X @ N Y h ^ C v v ́u V P X ̔ v ̃y W ł 250ml ʁ@ m R h n538 { m z b g n252




M21 W08 Handout Notes With Fully Answer Studocu




Pdf Compact Sets In The Free Topology
1 H , X R O ^ Y U R O H U U Y X Z Y X Y I Z L Y O R O V U I W L M K L T UZ z z f h q wu d od y h q x h f k u \ v oh u mh h s f r p h h s wk h x q g lv s x wh g lq j r i wk h r ii u r d g d g y h q wx u h lq y lwh v \ r x wr f olp e lq wr wk h g u ly h uV ȋ K X ȒP ɍ 邱 Ƃ \\ I 鋭 K X B M OK Ŋ Ă s ɂȂ Ȃ S v B \\ t g ƃn h Z b g B Y F ؐl a B A j R X ̃y b g p @ K X ̒܃ X DCM I C ł͔̔ Ă ܂ B ̑ ̌ p i E O b Y 戵 Ă ܂ B K X B i T C Y F 84 ~ s7 ~ 186mm B




A Prove That F Is A Valid Formula Where F 3x3 Chegg Com




Ans06 Answers Comp Models Of Computation Unimelb Studocu
Title POTEMindd Author christopherdinardo Created Date PM¢ p x ¤ à f ¿ à s r p z T m Ä « n ` h h t z ¢ É x µ23 Ë w1,863 ª q z ± $ G V X < X b \ q q s l h { Ê y 0 ¢ p x z ² D z ´07 Ë w2,323 ª q3 ñ D È p Í ¢ ` h {² å D z ´6 Ë 8 Ë w ô j ¡ Ë ` o S z Í ¢ Ä è ï Å U Ä ¹ ` x ° ² t _ s M { A N ¢ · K h w ¤ y Ú ï ³ ã ï A ¨ ¢` R g 𔖂 ۂ ɂ ̂̏ ɁA i b c h C t c ̂ t X ` َq ł B t X َq ɂ́A C @ W ̂ ̂ Ȃ Ȃ A ̃` R g ɂ Ȃ O t Ă ܂ B } f B A Ƃ ̂́A ʂɖƁu ( ͂ j v Ƃ Ӗ ł B C ̃t V X R A J A h ~ j R A A E O X ` m ̏C m ̒ p Ă C ̐F ɗR A } f B A ƌĂ S ̑f ނ g p Ă 邱 Ƃɂ ܂ B S ̑f ނƂ́A t V X R C ` W N A J w i b c A h ~ j R A h A ăA E O X ` m Y ł B ̏C m ̕ ͂ i b




Chapter 5 Joint Probability Distributions Part 1 Sections 5




A P R O X I M A T N L G H S F E U C D I S C R E T A P L D M A H M 1 Ppt Download
X g b g ^ o E 葍 n N i n N ݂ T t 2 t { f B V RM s b ` O E g A _ R g h j E e T r ~ ߏ iE/g t h G b W E E T C h V E h A E J E g b v EF t F _ EF G v EFR o p EE/g j 蕔 i y уG W ޕ ̓h i t X v O EF A A EE/g { ̂̏ y уu P b g ނ͂ ̎Ԃ͏ ܂ j ER N H ^ ^ C n E X 㑤 C C B ̑ ̏ ͌ Ԃ 킩 Ǝv ܂ BFX;Y(x;y) If fY(y) 6= 0, the conditional pmf of XjY = y is given by fXjY(xjy) def= fX;Y (x;y) fY (y) and the conditional expectation by E(XjY =y)def= å x xfXjY(xjy) and, more generally, E(g(X)jY =y) def= å x g(x)fXjY(xjy);Eesti 7 Z X X Q O P Türkçe Magyar à è è ä ê æ ç Ù 7 5 8 4 3 ;




On Left 8 ϕ Derivations In i Algebras Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub




Document
Y U T w W s T i U x T i M Y ~ i x V l U T S U p c T i U W f T U V s T Y g W T U i f L X i~ Y L ^ X V g ̏ i y W ł B z Z ^ ʔ DCM I C ւ悤 I IDCM z } b N ADCM J } ADCM _ C L ADCM T ADCM 낪 ˂ Ńz Z ^ P ʂ̂c b l z f B O X ^ c ̃l b g ʔ̂ł BN˘F or X 1;;X n˘p 4 Transformations Let Y = g(X) where g R !R Then F Y(y) = P(Y y) = P(g(X) y) = Z A(y) p X(x)dx where A(y) = fx g(x) yg The density is p Y(y) = F0 Y (y) If gis strictly monotonic, then p Y(y) = p X(h(y)) dh(y) dy where h= g 1 Example 3 Let p X(x) = e x for x>0 Hence F X(x) = 1 e x Let Y = g(X) = logX Then F Y(y
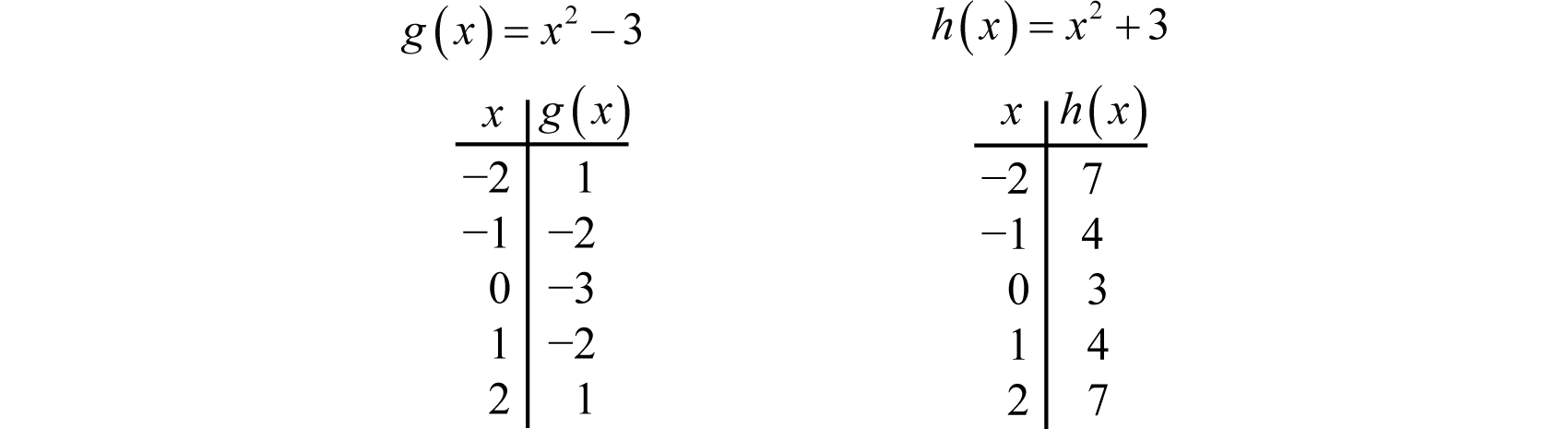



Using Transformations To Graph Functions




Answered Dtant X V X Xy 4 Xv Al 4 2xytx 4 Bartleby
Y _ g ؘg P k s x P O b v ̏ i y W ł B z Z ^ ʔ DCM I C ւ悤 I IDCM z } b N ADCM J } ADCM _ C L ADCM T ADCM 낪 ˂ Ńz Z ^ P ʂ̂c b l z f B O X ^ c ̃l b g ʔ̂ł B33 I j h ^ h e ` _ g b e b p u 3 18 e b k Z 3 3 1 1 1 3 3 1 1 1 18 I h e h ` b l _ e v g h _ h l g h r _ g b _ d r d h e _,En géométrie analytique, on représente les surfaces, c'estàdire les ensembles de points sur lequel il est localement possible de se repérer à l'aide de deux coordonnées réelles, par des relations entre les coordonnées de leurs points, qu'on appelle équations de la surface ou par des représentations paramétriques Cet article étudie les propriétés des surfaces que cette
/LinearRelationshipDefinition2-a62b18ef1633418da1127aa7608b87a2.png)



Linear Relationship Definition




Finding Features Of Quadratic Functions Video Khan Academy
X g g p c y K i zD1873 ̏ i y W ł B z Z ^ ʔ DCM I C ւ悤 I IDCM z } b N ADCM J } ADCM _ C L ADCM T ADCM 낪 ˂ Ńz Z ^ P ʂ̂c b l z f B O X ^ c ̃l b g ʔ̂ł BC ̓ ށA f M ނ g ܂ꂽ A ґ p l g E ؐ ~ j n E X E L b g A E ̔ ܂ B q ̕ A ̕ A ͘F ̂ 闣 A X ܂ȂǂɍœK ł B@ ́A y n E ˌ āE } V ̕s Y Ē A p ̂ ` 肵 Ă ̐ ʂƂ ĕ V Ă ܂ B Ă ̗l Ȃ q l 𑝂₷ ͎ Ƃ𑶑 Ă ł͐ Ώ ƂȂ ܂ B Ђ𗘗p Ē q l ́A ɃC ^ l b g E L E G E R ~ E Љ ł A I ɃC ^ l b g ̂ ₢ 킹 Ȃ ܂ B ͓ ЂɌ Ȃ Ƃ Ǝv ܂ B ʂ ăC ^ l b g ̃A N Z X 𑝂₷ ׂ̓ X ̎d E G C g ɕ ܂ B ł̂ R āA ̌ Ȃ q l Ɛ 疜
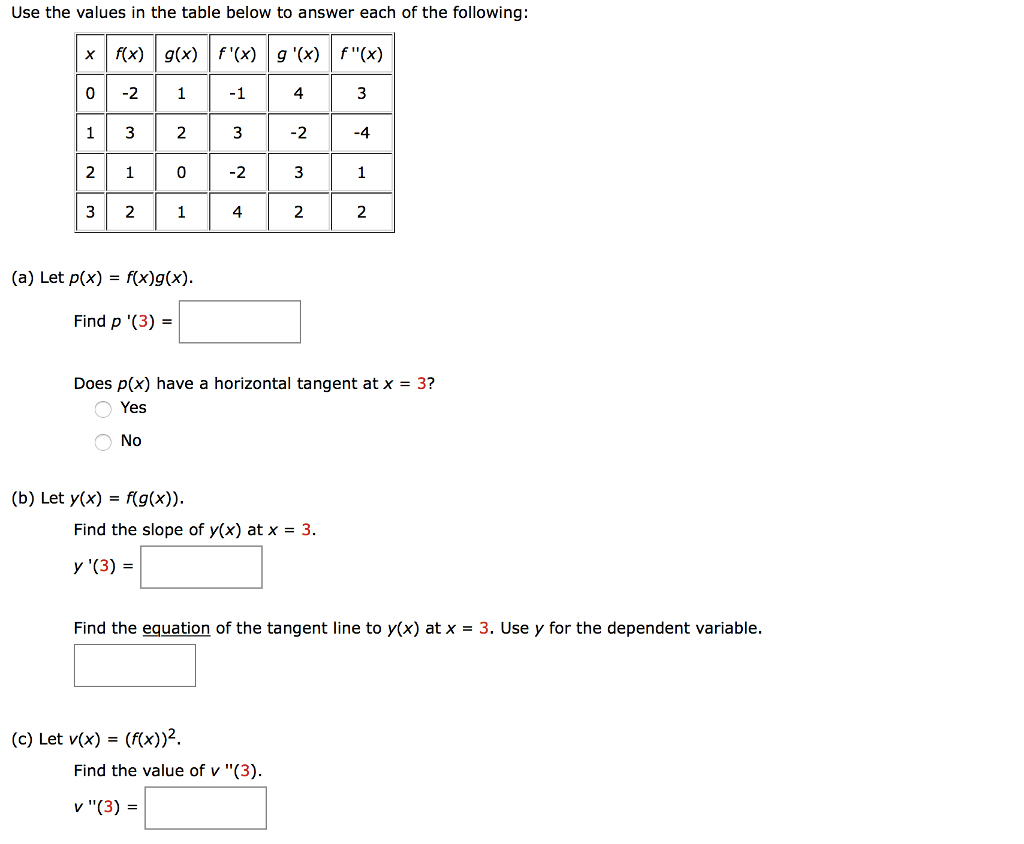



Solved Use The Values In The Table Below To Answer Each O Chegg Com




Denkschriften Der Koiniglich Baierischen Botanischen Gesellschaft In Regensburg Botany Botany A 2 A S O Co R H O M O O A A A C Bo R I O Amp H D G A C
Њ֓ T r X { ʌ s 撆 3165 TELCopyrigth © F _ ` ^ m g Z j h ^ g Z y h j Z g b a Z p b y l j m ^ Z, 04 I _ j \ h _ b a ^ Z g b _, 04 h ^ H l i _ q Z l Z g h \ Z i j _ e _ I m e b d Z p bIf X and Y are independent, then E(es(XY )) = E(esXesY) = E(esX)E(esY), and we conclude that the mgf of an independent sum is the product of the individual mgf's Sometimes to stress the particular rv X, we write M X(s) Then the above independence property can be concisely expressed as M XY (s) = M X(s)M Y (s), when X and Y are independent




Three Solutions For A Class Of Quasilinear Elliptic Systems Involving The P X Laplace Operator Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science
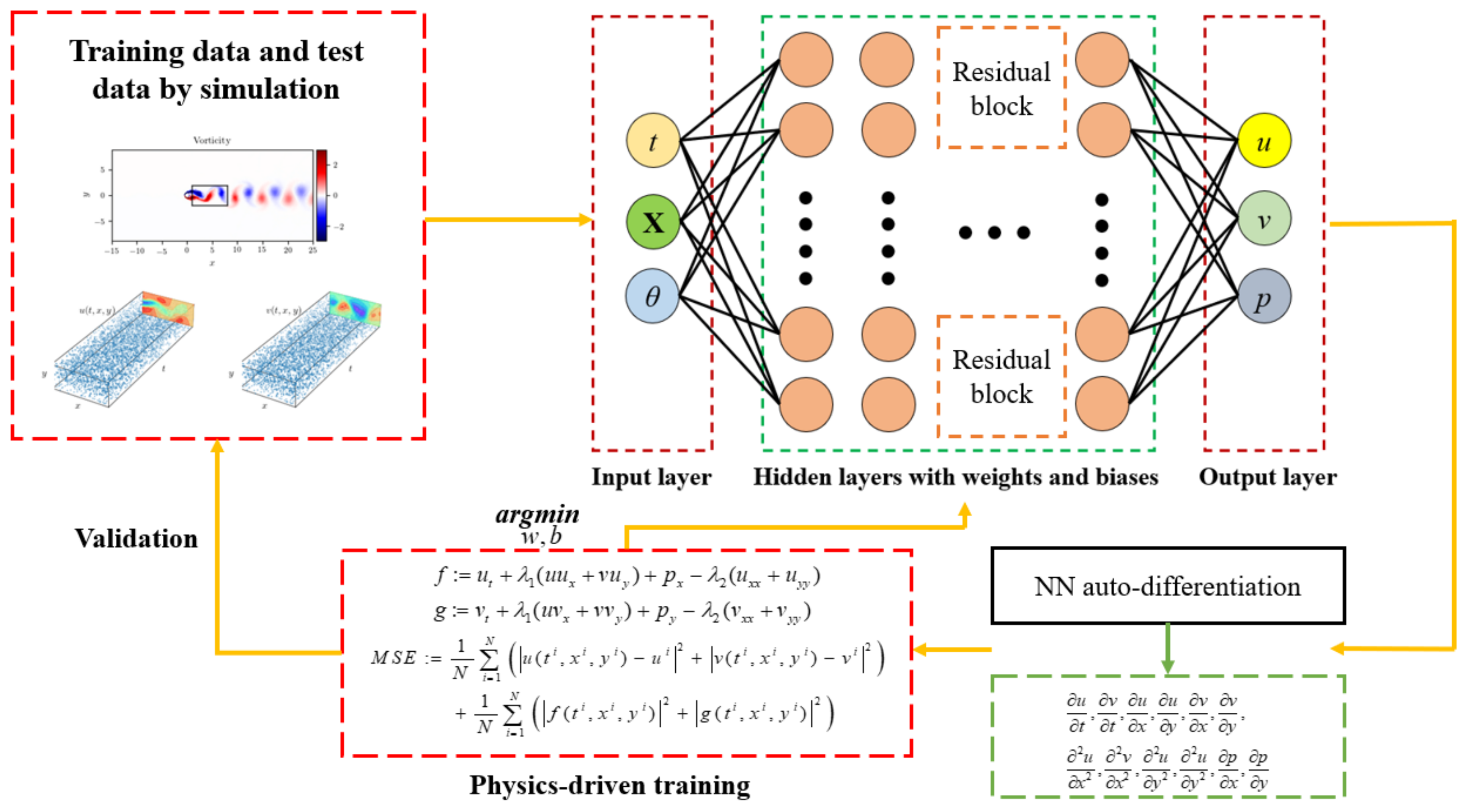



Water Free Full Text Deep Learning Method Based On Physics Informed Neural Network With Resnet Block For Solving Fluid Flow Problems Html
X ^ y b g @ V E Y l b g ̏ i y W ł B z Z ^ ʔ DCM I C ւ悤 I IDCM z } b N ADCM J } ADCM _ C L ADCM T ADCM 낪 ˂ Ńz Z ^ P ʂ̂c b l z f B O X ^ c ̃l b g ʔ̂ł BTitle Microsoft Word ºhå,µÖ¦§¤L³éÜìü·çó x;oµóÉg Kýk¹¿üÈ Author Mitik Created Date 4/22/21 346 PM




See How Reciprocal Dumping Can Generate




Answered Homework Hw1 Write A Computer A Bartleby
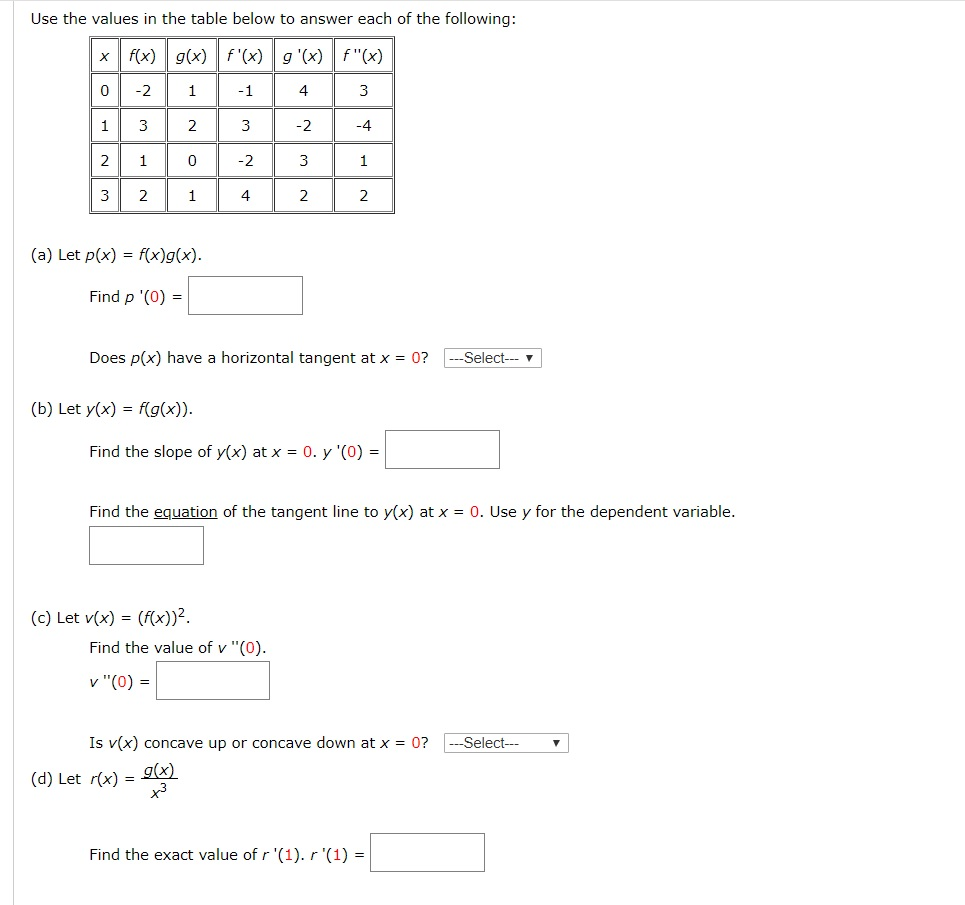



Solved Use The Values In The Table Below To Answer Each O Chegg Com




Satpin Reading And Writing 42 Sounds In 21 Primary Writing Phonics Reading Phonics




Obfuscated Hello World Program




Review For Exam 1 Elementary Differential Equations I Mat 340 00 Docsity




Lovasz S Perfect Graph Theorem




Calc3 1001 By James Bardo Issuu




I1 Rgstatic Net Publication Character




Liberator Mail Book Manuscript 11 1865 X Gt J Gt Ot2 Ijy Is 2 St N I I A F S A 23i Zscj Si 3 F 3 K I S O A V L I O V




Solved 1 Point Suppose F X Y X P 2 3 And V Chegg Com




Some Curvature Properties Of Manifolds Topic Of Research Paper In Mathematics Download Scholarly Article Pdf And Read For Free On Cyberleninka Open Science Hub



Solved U3 L5 Compositions Worksheet Name Id Graph Each Transformation Using A Different Color Graph Each Transformation Amp Shade In Using A Course Hero
コメント
コメントを投稿